Logistic Regression

Model introducation

Logistic Regression是一个分类模型，而不是回归模型. Logistic Regression回归的本质是：假设数据服从某个分布，然后用极大似然估计去做参数的估计.

Definition

设$X$是连续随机变量，$X$服从Logistic Regression是指$X$具有下列分布函数和密度函数：

$F(x) = P(X \leq x) = \frac{1}{1+e^{-(x-\mu)/\gamma}}$ $f(x) = F'(x) = \frac{e^{-(x-\mu)/\gamma}}{\gamma(1+e^{-(x-\mu)/\gamma})^2}$

使用Python matplotlib以及Numpy生成logistic的概率分布函数和概率密度函数图像：

# import packages
from matplotlib import pyplot as plt
import numpy as np

# define parameters
mu = 0
gamma = 1
x = np.linspace(-10,10,100)

# define function
def logistic(x):
    return np.exp(-(x-mu)/gamma)/(gamma * (1+np.exp(-(x-mu)/gamma))**2)

def distribution(x):
    return 1/(1+np.exp(-(x-mu)/gamma))

# plot figure
y = logistic(x)
z = distribution(x)
plt.title('Probability density function')
plt.plot(x,y)
plt.title('prabability distribution function')
plt.plot(x,z)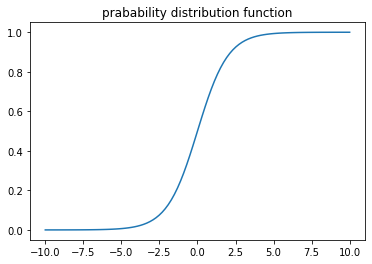

This is probability distribution function

对于概率分布函数，如果$\gamma$值越小，曲线在中心附近增长越快.

Binomial logistic regression model

二项逻辑回归模型有如下的条件概率分布：

$P(Y=1|x) = \frac{exp(w \cdot x+b)}{1+exp(w \cdot x +b)}$ $P(Y=0|x) = \frac{1}{1+exp(w \cdot x+b)}$

输入$x \in \mathbf{R}^{n}$，输出$Y\in{0,1}$, 参数$w\in \mathbf{R}^{n}, b \in \mathbf{R}$, $w \cdot x$是向量$w$和$x$的內积. 通过比较$P(Y=1|x)$和$P(Y=0|x)$大小，将$x$分类到概率大的那一类.

Definition of Odds

几率:

$\begin{aligned} & odds = \frac{p}{1-p}\\ & logit(p) = log\frac{p}{1-p}\\ & log\frac{P(Y=1|x)}{1-P(Y=1|x)}=w \cdot x + b \end{aligned}$

所以，在逻辑回归中，输出$Y$的对数几率是输入$x$的线性函数，这就是Logistic Regression. 线性函数$w\cdot x$的值越接近正无穷，$P(Y=1|x)$越接近1，反之，越接近0.

Parameter Estimation

给定已有的数据集$T={(x{1},y{1}), (x{2},y{2}), …, (x{n},y{n}) }$, 其中$x{i} \in \mathbf{R}, y{i} \in {0,1}$. 下面介绍使用极大似然估计法(MLE)进行参数估计.

Maximum Likelihood Estimation

MLE是一种参数估计方法，假设某事件满足某种概率分布，但是参数不知道，根据事件的结果推算出参数的取值. 一般来说，事件$A$发生的概率和某一未知参数$\theta$有关，$\theta$不同，则事件$A$发生的概率$P(A|\theta)$也不同.一般认为当事件$A$发生时，$\theta$的取值是使概率$P(A|\theta)$最大的那一个.\
MLE的一般过程：

写出似然函数
取对数，整理
求导
求解似然方程

似然函数为：

$\begin{aligned} L(\theta) & = f(x_{1}|\theta)f(x_{2}|\theta)\cdot\cdot\cdot f(x_{n}|\theta) \\ & = \prod_{i=1}^{N}[\pi(x_{i})]^{y_{i}}[1-\pi(x_{i})]^{1-y_{i}} \end{aligned}$

对数似然函数为：

$\begin{aligned} logL(\theta) & = \sum_{i=1}^{N}[y_{i}log\pi(x_{i})+(1-y_{i})log(1-\pi(x_{i}))] \\ & = \sum_{i=1}^{N}\bigg[y_{i}log\frac{\pi(x_{i})}{1-\pi(x_{i})}+log(1-\pi(x_{i})\bigg] \\ & = \sum_{i=1}^{N} \big[ y_{i}(w \cdot x_{i} + b) - log(1+exp(w\cdot x_{i} + b))\big] \end{aligned}$

求解下面的最优化问题, 得到$\theta$最优值(梯度下降法，拟牛顿法):

$max \{ logL(\theta) \}$

Multi-nominal logistic regression model

逻辑回归同时也可以用于多分类模型，假设输出是${1,2,…,K}$, 相应的概率为:

$P(Y=k|x)=\frac{exp(w_{k}\cdot x)}{1+\sum_{k=1}^{K-1}exp(w_{k}\cdot x)}, \quad k=1,2,...,K-1$

其中，$x\in \mathbf{R}^{n+1}, w_{k}\in \mathbf{R}^{n+1}$. 多元逻辑回归的参数估计方法和二元逻辑回归一样.